A list of trigonometric formulae and tables.

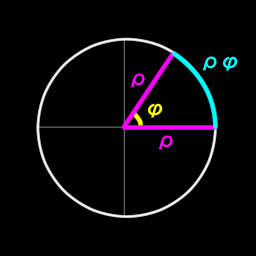
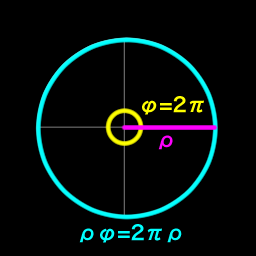
image of arc length image of circumference

Trigonometric functions in polar coordinate form- radius $\rho$, azimuth $\phi$. Hypotenuse is $\rho$, adjacent is x and opposite is y.

\[\begin{align} & y = \rho \sin \phi \\ & x = \rho \cos \phi \\ & \rho = \sqrt {x^2 + y^2} \\ & \phi = \arctan {\frac {y} {x}} & \phi = \operatorname{atan2}(y,x) \\ \end{align}\]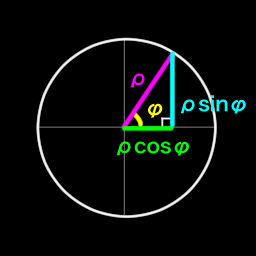

image of sin and cos

$\sin \phi$ and $\cos \phi$ get the $y$ and $x$ components of $\rho$.

\[\begin{align} & \sin {\phi} = \left( \frac {1} {\csc {\phi}} \right) = \left( \frac {y} {\rho} \right) & \left( \arcsin \frac {y} {\rho} \right) = \left( \sin ^{-1} \frac {y} {\rho} \right) = {\phi} \\ & \cos {\phi} = \left( \frac {1} {\sec {\phi}} \right) = \left( \frac {x} {\rho} \right) & \left( \arccos \frac {x} {\rho} \right) = \left( \cos ^{-1} \frac {x} {\rho} \right) = {\phi} \\ \end{align}\]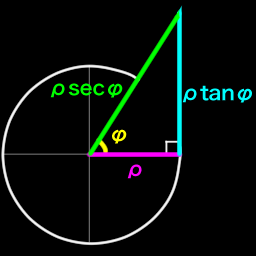

image of sec and tan

$\tan \phi$ and $\sec \phi$ get $y$ and $\rho$ from $x$.

\[\begin{align} & \tan {\phi} = \left( \frac {1} {\cot {\phi}} \right) = \left( \frac {y} {x} \right) & \left( \arctan \frac {y} {x} \right) = \left( \tan ^{-1} \frac {y} {x} \right) = {\phi} \\ & \sec {\phi} = \left( \frac {1} {\cos {\phi}} \right) = \left( \frac {\rho} {x} \right) & \left( \operatorname{arcsec} \frac {\rho} {x} \right) = \left( \sec ^{-1} \frac {\rho} {x} \right) = {\phi} \\ \end{align}\]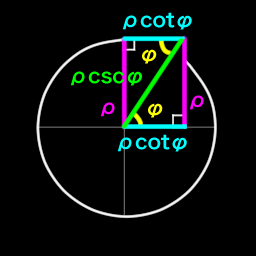

image of csc and cot

$\cot \phi$ and $\csc \phi$ get $x$ and $\rho$ from $y$.

\[\begin{align} & \cot {\phi} = \left( \frac {1} {\tan {\phi}} \right) = \left( \frac {x} {y} \right) & \left( \operatorname{arccot} \frac {x} {y} \right) = \left( \cot ^{-1} \frac {x} {y} \right) = {\phi} \\ & \ csc {\phi} = \left( \frac {1} {\sin {\phi}} \right) = \left( \frac {\rho} {y} \right) & \left( \operatorname{arccsc} \frac {\rho} {y} \right) = \left( \ csc ^{-1} \frac {\rho} {y} \right) = {\phi} \\ \end{align}\]

Trigonometric function values as a function of $\phi$. If the point is 0 or $\infty$, the $\pm$ and $\mp$ signs indicate the value of the function to either side of the specified point. Lower values of $\phi$ indicated by the sign on the top.

\[\begin{array}{c|lcr} \phi & \sin & \cos & \tan & \csc & \sec & \cot \\ \hline \frac {0} {2} \pi & \mp0 & +1 & \mp0 & \mp\infty & +1 & \mp\infty \\ \frac {1} {2} \pi & +1 & \pm0 & \pm\infty & +1 & \pm\infty & \pm0 \\ \frac {2} {2} \pi & \pm0 & -1 & \mp0 & \pm\infty & -1 & \mp\infty \\ \frac {3} {2} \pi & -1 & \mp0 & \pm\infty & -1 & \mp\infty & \pm0 \\ \frac {4} {2} \pi & \mp0 & +1 & \mp0 & \mp\infty & +1 & \mp\infty \\ \end{array} \\\]

Transposed version.

\[\begin{array}{c|lcr} \phi & \frac {0} {2} \pi & \frac {1} {2} \pi & \frac {2} {2} \pi & \frac {3} {2} \pi & \frac {4} {2} \pi \\ \hline \sin & \mp0 & +1 & \pm0 & -1 & \mp0 \\ \cos & +1 & \pm0 & -1 & \mp0 & +1 \\ \tan & \mp0 & \pm\infty & \mp0 & \pm\infty & \mp0 \\ \csc & \mp\infty & +1 & \pm\infty & -1 & \mp\infty \\ \sec & +1 & \pm\infty & -1 & \mp\infty & +1 \\ \cot & \mp\infty & \pm0 & \mp\infty & \pm0 & \mp\infty \\ \end{array}\]

Domain and range tables. Note that the range of the inverse trigonometric functions starts at either $-\frac \pi 2$ or 0, depending on the function.

\[\begin{array}{c|lcr} \text{Function} & \text{Domain} & \text{Range} \\ \hline \sin & \left(-\infty,+\infty\right) & \left[-1, +1\right] \\ \cos & \left(-\infty,+\infty\right) & \left[-1, +1\right] \\ \tan & \bigcup\limits_{k \in \mathbb{Z}} \left(\frac{(2k+1)\pi} {2},\frac{(2k+3)\pi} {2}\right) & \left(-\infty, +\infty\right) \\ \csc & \bigcup\limits_{k \in \mathbb{Z}} \left(k\pi,(k+1)\pi\right) & \left(-\infty,-1\right] \cup \left[+1,+\infty\right) \\ \sec & \bigcup\limits_{k \in \mathbb{Z}} \left(\frac{(2k+1)\pi} {2},\frac{(2k+3)\pi} {2}\right) & \left(-\infty,-1\right] \cup \left[+1,+\infty\right) \\ \cot & \bigcup\limits_{k \in \mathbb{Z}} \left(k\pi,(k+1)\pi\right) & \left(-\infty, +\infty\right) \\ \hline \sin^{-1} & \left[-1, +1\right] & \left[-\frac \pi 2,+\frac \pi 2\right]\\ \cos^{-1} & \left[-1, +1\right] & \left[0,+\pi\right] \\ \tan^{-1} & \left(-\infty, +\infty\right) & \left(-\frac \pi 2,+\frac \pi 2\right) \\ \csc^{-1} & \left(-\infty,-1\right] \cup \left[+1,+\infty\right) & \left[-\frac \pi 2,0\right) \cup \left(0,+\frac \pi 2\right] \\ \sec^{-1} & \left(-\infty,-1\right] \cup \left[+1,+\infty\right) & \left[0, +\frac \pi 2\right) \cup \left(+\frac \pi 2,\pi\right] \\ \cot^{-1} & \left(-\infty, +\infty\right) & \left(0,+\pi\right) \\ \end{array}\]

Reciprocal and quotient identities.

\[\begin{align} & \tan = \left( \frac {1} {\cot \phi} \right) = \left( \frac {\sin \phi} {\cos \phi} \right) = \left( \frac {\sec \phi} {\csc \phi} \right) = \sin \phi \cdot \sec \phi = \left( \frac {1} {\csc \phi \cdot \cos \phi} \right) =\left( \frac {y} {\rho} \cdot \frac {\rho} {x} \right) = \left( \frac {y} {x} \right) \\ & \cot = \left( \frac {1} {\tan \phi} \right) = \left( \frac {\cos \phi} {\sin \phi} \right) = \left( \frac {\csc \phi} {\sec \phi} \right) = cos \phi \cdot \csc \phi = \left( \frac {1} {\sec \phi \cdot \sin \phi} \right) = \left( \frac {x} {\rho} \cdot \frac { \rho} {y} \right) = \left( \frac {x} {y} \right) \\ & \sin = \left( \frac {1} {\csc \phi} \right) = \left( \frac {\tan \phi} {\sec \phi} \right) = \left( \frac {\cos \phi} {\cot \phi} \right) = \tan \phi \cdot \cos \phi = \left( \frac {1} {\cot \phi \cdot \sec \phi} \right) = \left( \frac {y} {x} \cdot \frac {x} {\rho} \right) = \left( \frac {y} {\rho} \right) \\ & \csc = \left( \frac {1} {\sin \phi} \right) = \left( \frac {\sec \phi} {\tan \phi} \right) = \left( \frac {\cot \phi} {\cos \phi} \right) = \sec \phi \cdot \cot \phi = \left( \frac {1} {\cos \phi \cdot \tan \phi} \right) = \left( \frac {\rho} {x} \cdot \frac {x} {y} \right) = \left( \frac {\rho} {y} \right) \\ & \cos = \left( \frac {1} {\sec \phi} \right) = \left( \frac {\cot \phi} {\csc \phi} \right) = \left( \frac {\sin \phi} {\tan \phi} \right) = \cot \phi \cdot \sin \phi = \left( \frac {1} {\tan \phi \cdot \csc \phi} \right) = \left( \frac {x} {y} \cdot \frac {y} {\rho} \right) = \left( \frac {x} {\rho} \right) \\ & \sec = \left( \frac {1} {\cos \phi} \right) = \left( \frac {\csc \phi} {\cot \phi} \right) = \left( \frac {\tan \phi} {\sin \phi} \right) = \csc \phi \cdot \tan \phi = \left( \frac {1} {\sin \phi \cdot \cot \phi} \right) = \left( \frac {\rho} {y} \cdot \frac {y} {x} \right) = \left( \frac {\rho} {x} \right) \\ \end{align}\]

Cofunction identities. All take the form $ \operatorname{f} \left( \frac {\pi} {2} - {\phi} \right) = \operatorname{cof} {\phi}$ and vice versa.

\[\begin{align} & \sin \left( \frac {\pi} {2} - {\phi} \right) = \cos {\phi} & \cos \left( \frac {\pi} {2} - {\phi} \right) = \sin {\phi} \\ & \tan \left( \frac {\pi} {2} - {\phi} \right) = \cot {\phi} & \cot \left( \frac {\pi} {2} - {\phi} \right) = \tan {\phi} \\ & \sec \left( \frac {\pi} {2} - {\phi} \right) = \csc {\phi} & \csc \left( \frac {\pi} {2} - {\phi} \right) = \sec {\phi} \\ \end{align}\]

Odd and even function identities. $\cos$ and $\sec$ are even. The rest are odd. \(\begin{align} & \sin ({- \phi}) = - \sin ({\phi}) & \csc ({- \phi}) = - \csc ({\phi}) \\ & \cos ({- \phi}) = \cos ({\phi}) & \sec ({- \phi}) = \sec ({\phi}) \\ & \tan ({- \phi}) = - \tan ({\phi}) & \cot ({- \phi}) = - \cot ({\phi}) \\ \end{align}\)

Pythagorean identities. These cover all three sets of functions.

\[\begin{align} & \sin^2 \phi + \cos^2 \phi = 1 \\ & 1 + \tan^2 \phi = \sec^2 \phi \\ & 1 + \cot^2 \phi = \csc^2 \phi \\ \end{align}\]

Trigonometric identities.

\[\begin{align} & \cos (\phi) \cos (\theta) = \left( \frac {\cos (\phi+\theta) + \cos (\phi-\theta)} {2} \right) \\ & \sin (\phi) \sin (\theta) = \left( \frac {\cos (\phi-\theta) - \cos (\phi+\theta)} {2} \right) \\ & \sin (\phi) \cos (\theta) = \left( \frac {\sin (\phi+\theta) + \sin (\phi-\theta)} {2} \right) \\ & \cos (\phi) \sin (\theta) = \left( \frac {\sin (\phi+\theta) - \sin (\phi-\theta)} {2} \right) \\ & \cos (\phi) \sin (\theta) = \sin (\theta) \cos (\phi) \\ \\ & \sin (\phi) + \sin (\theta) = 2 \sin \left( \frac {\phi + \theta} {2} \right) \cos \left( \frac {\phi - \theta} {2} \right) \\ & \sin (\phi) - \sin (\theta) = 2 \cos \left( \frac {\phi + \theta} {2} \right) \sin \left( \frac {\phi - \theta} {2} \right) \\ & \cos (\phi) + \cos (\theta) = 2 \cos \left( \frac {\phi + \theta} {2} \right) \cos \left( \frac {\phi - \theta} {2} \right) \\ & \cos (\phi) - \cos (\theta) = -2 \sin \left( \frac {\phi + \theta} {2} \right) \sin \left( \frac {\phi - \theta} {2} \right) \\ \end{align}\]

Sum and difference formulas.

\[\begin{align} & \sin(\phi + \theta) = \sin\phi \cos\theta + \cos\phi \sin\theta \\ & \sin(\phi - \theta) = \sin\phi \cos\theta - \cos\phi \sin\theta \\ & \cos(\phi + \theta) = \cos\phi \cos\theta - \sin\phi \sin\theta \\ & \cos(\phi - \theta) = \cos\phi \cos\theta + \sin\phi \sin\theta \\ & \tan(\phi + \theta) = \left( \frac {\tan\phi + \tan\theta} {1 - \tan\phi\tan\theta} \right) \\ & \tan(\phi - \theta) = \left( \frac {\tan\phi - \tan\theta} {1 + \tan\phi\tan\theta} \right) \\ \end{align}\]

Double angle identities.

\[\begin{align} & \sin(2 \phi) = 2 \sin\phi \cos\phi \\ & \cos(2 \phi) = \cos^2 \phi - \sin^2 \phi \\ & \cos(2 \phi) = 2 \cos^2 \phi - 1 \\ & \cos(2 \phi) = 1 - 2 \sin^2 \phi \\ & \tan(2 \phi) = \left( \frac {2 \tan \phi} {1 - \tan^2 \phi} \right) \\ \end{align}\]

Half angle identities.

\[\begin{align} & \sin \left( \frac {\phi} {2} \right) = \left( \frac {1} {\csc (\phi / 2)} \right) = \pm \sqrt{ \frac {1 - \cos \phi} {2} } \\ & \cos \left( \frac {\phi} {2} \right) = \left( \frac {1} {\sec (\phi / 2)} \right) = \pm \sqrt{ \frac {1 + \cos \phi} {2} } \\ & \tan \left( \frac {\phi} {2} \right) = \left( \frac {1} {\cot (\phi / 2)} \right) = \frac {\sin \phi} {1 + \cos \phi} = \frac {1 - \cos \phi} {\sin \phi} \\ & \csc \left( \frac {\phi} {2} \right) = \left( \frac {1} {\sin (\phi / 2)} \right) = \pm \sqrt{ \frac {2} {1 - \cos \phi} } \\ & \sec \left( \frac {\phi} {2} \right) = \left( \frac {1} {\cos (\phi / 2)} \right) = \pm \sqrt{ \frac {2} {1 + \cos \phi} } \\ & \cot \left( \frac {\phi} {2} \right) = \left( \frac {1} {\tan (\phi / 2)} \right) = \frac {1 + \cos \phi} {\sin \phi} = \frac {\sin \phi} {1 - \cos \phi} \\ \end{align}\]

Power reducing identities.

\[\begin{align} & \sin^2 \phi = \left( \frac {1} {csc^2 \phi} \right) = \left( \frac {1 - \cos 2\phi} {2} \right) \\ & \cos^2 \phi = \left( \frac {1} {sec^2 \phi} \right) = \left( \frac {1 + \cos 2\phi} {2} \right) \\ & \tan^2 \phi = \left( \frac {1} {cot^2 \phi} \right) = \left( \frac {1 - \cos 2\phi} {1 + \cos 2\phi} \right) \\ & \csc^2 \phi = \left( \frac {1} {sin^2 \phi} \right) = \left( \frac {2} {1 - \cos 2\phi} \right) \\ & \sec^2 \phi = \left( \frac {1} {cos^2 \phi} \right) = \left( \frac {2} {1 + \cos 2\phi} \right) \\ & \cot^2 \phi = \left( \frac {1} {tan^2 \phi} \right) = \left( \frac {1 + \cos 2\phi} {1 - \cos 2\phi} \right) \\ \end{align}\]

Spherical coordinates- radius $\rho$, inclination $\theta$, azimuth $\phi$.

\[\begin{align} & x = \rho \sin \theta \cos \phi \\ & y = \rho \sin \theta \sin \phi \\ & z = \rho \cos \theta \\ & \rho = \sqrt {x^2 + y^2 + z^2} \\ & \theta = \arccos {\frac {z} {\sqrt {x^2 + y^2 + z^2}}} = \arccos {\frac {z} {\rho}} \\ & \phi = \arctan {\frac {y} {x}} \\ \end{align}\]

Polar form of a complex number.

\[\begin{align} & z = a + bi \\ & z = \rho \cos \phi + (\rho \sin \phi)i \\ & z = \rho (\cos \phi + i \sin \phi) \\ & \rho = |z| = \sqrt {a^2 + b^2} \\ & a = \rho \cos \phi \\ & b = \rho \sin \phi \\ & \phi = \tan^{-1} \left( \frac b a \right), 0 \le a \\ & \phi = \tan^{-1} \left( \frac b a \right) + \pi, a \lt 0 \\ & z_1 z_2 = r_1 r_2 (\cos(\phi_1 +\phi_2) + i \sin(\phi_1 + \phi_2)) \\ & \left( \frac {z_1} {z_2} \right) = \left( \frac {r_1} {r_2} \right) (\cos(\phi_1 -\phi_2) + i \sin(\phi_1 - \phi_2)) \\ \end{align}\]

DeMoivre’s Theorem. $z^n$ is a complex number raised to the power of $n$.

\[\begin{align} &z^n = \left[\rho(\cos \phi + i \sin \phi)\right]^n = \rho^n \left(\cos(n\phi)+i \sin(n\phi)\right) \\ \end{align}\]

The nth root of a number. There are $n$ complex roots for positive values of $n$. $k$ is used to calculate each root in turn.

\[\begin{align} & z = \rho \left( \cos {\phi} + i \sin {\phi} \right) \\ & ^n\sqrt z_k = z^{1/n}_k = \rho^{1/n} \left( \cos \left( \frac {\phi} {n} + \frac {2\pi k} {n} \right) + i \sin \left( \frac {\phi} {n} + \frac {2\pi k} {n} \right) \right) & 0\lt n; k=0,1,2,\cdots,n-1\\ \end{align}\]

Orthogonal decomposition.

\[\begin{align} & \vec{v}^\parallel = \operatorname{proj}_{\vec \rho} \vec{v} = \left( \frac {\vec{v} \cdot \vec{\rho}} {\vec{\rho} \cdot \vec{\rho}} \right) \vec {\rho} \\ & \vec{v}^\bot = \vec {v} - \vec{v}^\parallel \\ \end{align}\]

Triangulation.

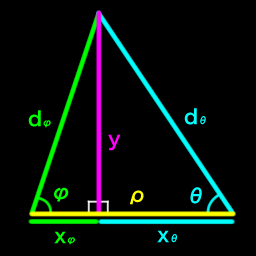
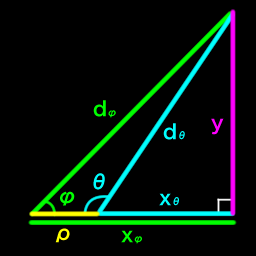
image of triangulation image of triangualtion with obtuse angle

Angles from two locations- $\phi$, $\theta$. Baseline distance between locations- $\rho$. Shortest distance from baseline to target object- $y$. Distance along baseline from respective measuring points to point in front of target object- $x_\phi$, $x_\theta$. Distance from respective measuring points to target object- $d_\phi$, $d_\theta$. NOTE: $\phi$ and $\theta$ are interior angles.

\[\begin{align} & y = \rho \sin \phi \sin \theta \csc (\phi + \theta) & y = \left( \frac {\rho \sin \phi \sin \theta} {\sin (\phi + \theta)} \right) \\ & x_\phi = \rho \cos \phi \sin \theta \csc (\phi + \theta) & x_\phi = \left( \frac {\rho \cos \phi \sin \theta} {\sin (\phi + \theta)} \right) \\ & x_\theta = \rho \sin \phi \cos \theta \csc (\phi + \theta) & x_\theta = \left( \frac {\rho \sin \phi \cos \theta} {\sin (\phi + \theta)} \right) \\ & d_\phi = \rho \sin \theta \csc (\phi + \theta) & d_\phi = \left( \frac {\rho \sin \theta} {\sin (\phi + \theta)} \right) \\ & d_\theta = \rho \sin \phi \csc (\phi + \theta) & d_\theta = \left( \frac {\rho \sin \phi} {\sin (\phi + \theta)} \right) \\ & \theta = \pi - \theta_{\text{exterior angle}} \\ \end{align}\]

Tangent line on circle of radius $\rho$ at angle $\phi$, simple rotations and mirrors.

\[\begin{align} & y = -\cot^{-1}\phi (x - \rho \cos \phi) + \rho \sin \phi & \text{$\phi$ tangent line} \\ & y = \tan^{-1}\phi (x + \rho \sin \phi) + \rho \cos \phi & \text{$\phi+\frac {\pi} {2}$ tangent line, quarter revolution CCW} \\ & y = \tan^{-1}\phi (x - \rho \sin \phi) - \rho \cos \phi & \text{$\phi-\frac {\pi} {2}$ tangent line, quarter revolution CW} \\ & y = -\cot^{-1}\phi (x + \rho \cos \phi) - \rho \sin \phi & \text{$\phi \pm\pi$ tangent line, half revolution} \\ & y = \cot^{-1}\phi (x + \rho \cos \phi) + \rho \sin \phi & \text{$\pi-\phi$ tangent line, mirror along $y=0$} \\ & y = \cot^{-1}\phi (x - \rho \cos \phi) - \rho \sin \phi & \text{$-\phi$ tangent line, mirror along $x=0$} \\ & y = -\tan^{-1}\phi (x - \rho \sin \phi) + \rho \cos \phi & \text{$\frac {\pi} {2} - \phi$ or $-\frac {3\pi} {2} - \phi$ TL, mirror along $y=x$} \\ & y = -\tan^{-1}\phi (x + \rho \sin \phi) - \rho \cos \phi & \text{$\frac {3\pi} {2} - \phi$ or $-\frac {\pi} {2} - \phi$ TL, mirror along $y=-x$} \\ \end{align}\]